- tags: LeetCode,backtracking
- source: https://leetcode.com/problems/n-queens/
一旦一个 Queue 被放置,那么横轴、纵轴、对角线都不再允许放置。我们按行进行遍历,所以我们需要跟踪以下位置是否已经放置 Queue:
- 纵轴(Column):cols
- 主对角线(Positive Diagonal):posDiag
- 次对角线(Negative Diagonal):negDiag
纵轴很好记录,但是对角线比较困难,我们先来看一下对角线的特征,假设横轴为 r 纵轴为 c ,
r - c 在正对角线是一致的:
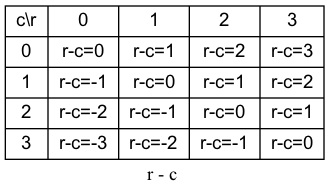
斜对角线 r + c 是一致的:

class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
for (int r = 0; r < n; r++) {
string col = string(n, '.');
track.push_back(col);
}
backtracking(0, n);
return res;
}
private:
set<int> cols; // c
set<int> posDiag; // r - c
set<int> negDiag; // r + c
vector<vector<string>> res;
vector<string> track;
void backtracking(int r, int n) {
if (r == n) {
res.push_back(track);
return;
}
for (int c = 0; c < n; c++) {
if (cols.find(c) != cols.end() || posDiag.find(r - c) != posDiag.end() || negDiag.find(r + c) != negDiag.end()) {
continue;
}
cols.insert(c);
posDiag.insert(r - c);
negDiag.insert(r + c);
track[r][c] = 'Q';
backtracking(r + 1, n);
track[r][c] = '.';
cols.erase(c);
posDiag.erase(r - c);
negDiag.erase(r + c);
}
}
};
结果
[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
一些想明白的问题:
- 为什么没有 Q 出现在第一行第一列的情况?因为没有走到最后一行(r == n)
- 怎么出现的两个结果?这个要看回溯过程。
回溯过程:
- 在每一列放置 Q 之后都会陷入下一行的递归中。
- 相当于以第一行的每一列进行遍历,依次穷举剩下行的每一列的可能性。
- 一旦一条路径走到头(r == n)说明有结果,还是回溯过程,接着进行下一列的可能回到 1. 继续